Be Sure to Drink Your Ovaltine

This year marks the 40th anniversary of The Christmas Story, one of my favorite Christmas movies ever made. I don’t think I’m spoiling anything here since this runs 24 hours a day on a ton of stations in December, but if I am, go watch it first.

One scene is especially interesting to folks interested in cryptography — the Orphan Annie’s Decoder “Ring” (search it, tons of sites go full pedantic that it’s a decoder “pin”).

Ralphie Parker is a child in the movie and saves up enough Ovaltine labels to join the Little Orphan Annie’s Secret Society (a real society that would mark their decoder pins with “SS” for “Secret Society” until 1939. I wonder why that changed?!)

In the movie, he tunes to a radio program… Maybe because they forgot to pay their cable bill or whatever, and the host calls out a series of numbers.

Because this was never predicted to have the cult following it does or do so well at the box office, it likely was recorded on tape, which means that we’re about to rock out with our pixels out. All four of them.

Now I did my work and searched for a clear photo of these numbers, and I couldn’t find them. Forbes already did something similar to what I plan to do here, so if you want to read a shitty website behind a paywall, here’s your chance.

I opted to go to a different site with a shitty API policy, Reddit. Somebody went through all the work I’m going to do here, and they got the numbers albeit easier to read:

12 11 2 3 25 11 4 24 16 25 18 23 21 6 24 3 25 24 5 9 19 4 18 23 11

I’m going to see if I can decode this, and before you say “Oh Bob, another stupid topic for a blog that nobody will read”, you’re right, except that the Department of Defense disagrees.

I figured when I watched this that this was a simple substitution cipher, like Caesar Cipher

In the movie, they mention “Set your decoder ring to B2”, so immediately in my head, I figured they ship the ring like this:

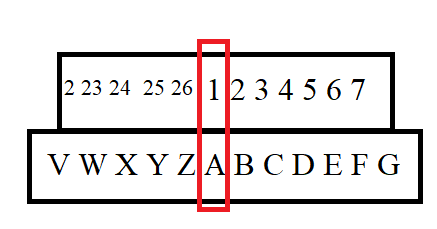
Designed on my PC with Microsoft Paintbrush

So, when they say “Set it to B2”, well that would be like lining up the two halves with A=1, B=2, C=3 (etc).

That would make decoding this stupid easy. Let’s do that.

First, let’s make up a look up table.

12	11	2	3	25	11	4	24	16	25	18	23	21	6	24	3	25	24	5	9	19	4	18	23	11
L	K	B	C	Y	K	D	X	P	Y	R	W	U	F	X	C	Y	X	E	I	S	D	R	W	K

cLEARLY NOT THE CODE >capslock<. So, Maybe it wasn’t B2, maybe it was C2, D2, E2, G2, P2, T2, V2, or Z2. They’re all pretty close sounding to B2, but it’s already late and I’m not looking to do an exhaustive search.

We have an amazing advantage:

12	11	2	3	25	11	4	24	16	25	18	23	21	6	24	3	25	24	5	9	19	4	18	23	11
B	E	S	U	R	E	T	O	D	R	I	N	K	Y	O	U	R	O	V	A	L	T	I	N	E

We have the code and the output it generates. First things first, if you count up the numbers you get 25. You also get 25 if you count up the letters. So this is a substitution cipher (meaning one character or value equates to the other), and if we look at the most common letter in the English language “E”, we see three occurrences and they both equate to “11”. This means the match is 1=1, once you compromise a letter / number (for rotor position B2, at least) you will always know what you’re dealing with.

Frequency Analysis

Many, MANY years ago, I took a decent sized forum site I ran and computed a live frequency analysis against the data set. By far English, and somewhat nerd, it was pretty accurate. But this was nine years ago and I can’t find anything but this screenshot (no graph) in the archive:

The image block is missing and I can’t find a copy of it. That’s fine because I can just find an image… Ah, here we go:

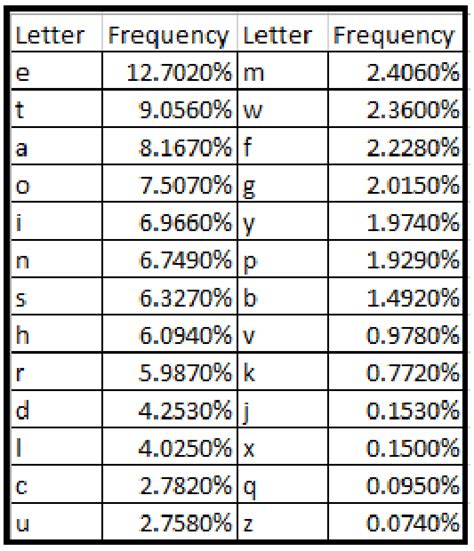
This is sorted by letter frequency, and E is by far the most common. So, I took the code and ditched the spaces, and added a leading zero to all single digit numbers (this way each value takes up two characters, or a “bigram”):

12110203251104241625182321062403252405091904182311

Then I slapped that bad boy into this site and got this:

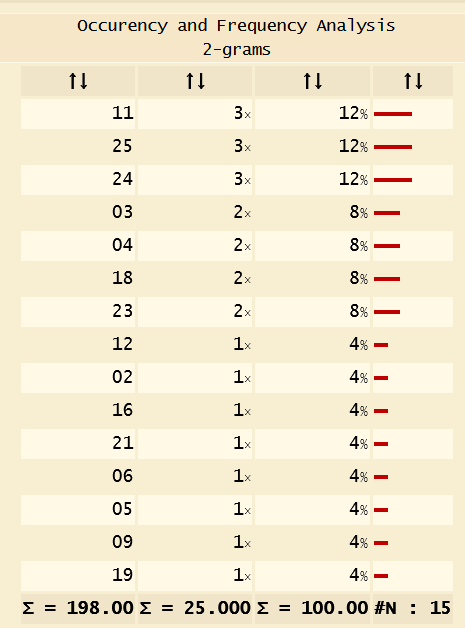
Annoyingly, our sample set absolutely sucks., you can see we have 15 unique values across 25 total values, even still, this sample size is way too small to be useful. See, 11, 25, and 24 are showing as used three times each in the string, corresponding to E, R and O respectively. If we look at the frequency chart, E is indeed #1, as we expect. O is #4, but R is #9. The sample size we have just isn’t enough to figure it out from just the ciphertext using this method. Now, if we were to capture perhaps dozens of these sessions, and the ring/pin was always set to B2, then we would have the answer.

I guess the next idea is to do a distance calculation. A=1, B=2 (see notepad above).

We know that E = 11 based on the data we have, so that should mean that F = 12, G = 13. Instead, B = 12, D = 16, and E = 11. Now we know that either the number reel isn’t sequential (Not 1, 2, 3, … 26) and / or the letter reel isn’t sequential (A, B, C … Z).

We can make an assumption that the number wheel IS sequential, seeing as the radio host uses that as an index, to improve seek time you’d want that to be in order so a logical human can decode it faster.

Now we do have even more information from images in the movie, but I’m trying to avoid cheating here (so far). Lets figure out what we do know about the ring:

1	?
2	S
3	U
4	T
5	V
6	Y
7	?
8	?
9	A
10	?
11	E
12	B
13	?
14	?
15	?
16	D
17	?
18	I
19	L
20	?
21	K
22	?
23	N
24	O
25	R
26	?

Just looking at this, was the code really B2? I see S2 or B12… And I’m not just adjusting the narrative to fit my confusion, extremely reputable sources of information like Forbes and Reddit (that would never adjust narrative) even point this out… And my chart above agrees with them.

To reiterate, we have 15/25 figured out from this one message (60%). Referencing the frequency chart (again):

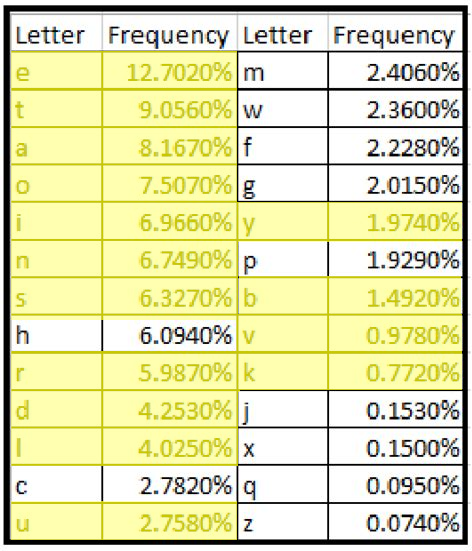
Yellow is what we have figured out for sure, we have ~85% of the most common letters (left side) on hand. What this means is, if they change the rotor position to another number and we capture that message, we can use the two sets of data to build better coverage of the alphabet, eventually being able to simply infer the rest of the details.

In the Forbes article, you’ll notice they make a platitude about Vingenere cipher and suggest the word MILK. What this means is that our message would be as follows:

BESURETODRINKYOUROVALTINE

++++++++++++++++++++

MILKMILKMILKMILKMILKMILKM

The first column here would use the “B” from the top string, plus the “M” from the bottom, because we know the ciphertext starts with 12, we have to assume that B+M=12 if that is the system. Let’s try that with a more common letter. We know E=11, so the next letter is E+I=11… a few letters later, the “E” in “SURE” lines up again with E+I, okay, dude might be onto something…. The last E (in Ovaltine) is I+M, and that adds up to…11?

If that’s the case, the E=M, so lets simplify and make all the “M” to “I”:

BESURETODRINKYOUROVALTINE

++++++++++++++++++++

IILKIILKIILKIILKIILKIILKI

Now lets take the “O” from “TO” and “OVALTINE”, we get O+K = 24 and O + I = 24.

This means that E = M = K… It’s not adding up anymore — we’re implying that we’re using a key here to add a repeating sequence, but we know a few things about this: It’s a decoder ring/pin and there are digits / letters on the edge of it. You’d need to know the key “MILK” to decode it and it would be stupidly big they’d have to drop ship the decoder ring itself.

It’s Midnight

I’m a night owl, I need to fix that. At least for now, I’m going to close with a different view of what we know of the ring:

SUTVY__A_EB___D_IL_K_NOR

The underscores are obviously what we don’t know. More likely than not, there is no magic formula and they just picked these out of a hat. Quickly, before I stop this blog, let’s compare distances:

A <-> B = 2 (no wrapping) or 28 (wrapping)

D <-> E = -3 (no wrapping) or 18 (wrapping)

N <-> O = 0 or 24

“R>>>SUTVY” feels weirdly close as well

I don’t immediately see a way to get the rest of the decoder wheel from this knowledge, but maybe we can with images? I still owe you an LMC disassembly blog, so I’ll revisit this sometime later.